Ecc Key Pair Generation Online
The key generation on this website is done client-side only. This means the key pairs are generated entirely in your web browser and they never leave your computer. This website never sees any key related data or the key itself. Elliptic Curve Cryptography (ECC) is an approach to public-key cryptography based on the algebraic structure of. The Generate ECC Key Pair (OPM, QC3GENECC; ILE, Qc3GenECCKeyPair) API generates a random ECC key pair given a set of domain parameters to be used with elliptic curve cryptographic algorithms such as ECDSA. Information on cryptographic standards can be found in Create Algorithm Context (OPM, QC3CRTAX; ILE, Qc3CreateAlgorithmContext) API. This ECC key pair generation reference design shows how to enable the ECC key pair generation engine to generate the public key and private key. The ECDSA design is used for the verification of the generated keys.
- Install OpenSSL. When the executable in your path, enter this command to generate a private key: openssl ecparam -genkey -name secp256k1 -noout -out myprivatekey.pem To create the corresponding public key, do this: openssl ec -in myprivatekey.pem -pubout -out mypubkey.pem This will give you both keys in PEM format.
- To generate an EC key pair the curve designation must be specified. Note that JOSE ESxxx signatures require P-256, P-384 and P-521 curves (see their corresponding OpenSSL identifiers below). Elliptic Curve private + public key pair for use with ES256 signatures: openssl ecparam -genkey -name prime256v1 -noout -out ec256-key-pair.pem.
- Key pairs include the generation of the public key and the private key. Because of this part of the process, RSA has often been described as the first public-key digital security system. Once the public key is generated, it is transmitted over an unsecured channel, but the private key remains secret and is not shared with anyone.
Get familiar with elliptic curve private and public key pairs.
Join the DZone community and get the full member experience.
Join For FreeAn EC (Elliptic Curve) key-pair is a pair of a private and public key constructed from a given subgroup generator in a given elliptic curve group.
Here are the steps to generate an EC private and public key pair:
1. Alice selects an elliptic curve subgroup defined by a set of domain parameters, (p,a,b,G,n,h):
2. Alice selects a private number, d, and puts it together with domain parameters as the private key:
Ecc Key Pair Generation Online Shopping
3. Alice performs the scalar multiplication of Q = d*G and puts it together with domain parameters as the public key:
Actually, the order of the subgroup, n, and the cofactor of the subgroup, h, are not really important because they can be derived from the generator, G.
Also, if the subgroup (or domain parameters) is publicly known to everyone, we can simply refer to d as the private key and Q as the public key.
For example, if Alice decides to use the subgroup generated by G = (15, 13) in the elliptic curve group of E17(0, 7). The domain parameters will be:
If Alice selects d = 11 as the private number, her private key will be:
Alice then calculates Q = d*G = 11*(15, 3) = (10, 2). Her key public key will be:
Opinions expressed by DZone contributors are their own.
Widely-accepted asymmetric key algorithms have superseded their predecessors, providing better security and performance in response to need. While there are many algorithms that have been developed over the years in computer science, the ones that have received the most widespread support are RSA, DSA, and now ECC, which can be combined with RSA for even more secure protection.
In order for a public key cryptographic system to work, you need to have a set of algorithms that is easy to process in one direction, but difficult to move in the other direction. The standard has been in use since the 1970s depends upon the multiplication of two large prime numbers.
Difference Between Diffie-Hellman, RSA, DSA, ECC and ECDSA
Let’s look at following major asymmetric encryption algorithms used for digitally sing your sensitive information using encryption technology.
Diffie-Hellman:
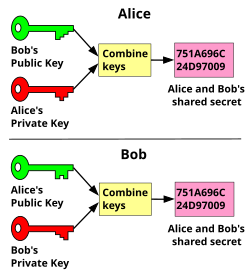
The first prime-number, security-key algorithm was named Diffie-Hellman algorithm and patented in 1977. The Diffie-Hellman algorithm is non-authenticated protocol, but does require the sharing of a “secret” key between the two communicating parties. The two parties agree on an arbitrary starting number that they share, then each selects a number to be kept private.
In the critical exchange, each party multiplies their secret number by the public number, and then they exchange the result. When each multiplies the exchanged numbers with their private numbers, the result should be identical, providing provenance between the parties. It is difficult, computationally speaking, for a third-party listener to derive the private numbers.
However, in the absence of authentication, Diffie-Hellman is vulnerable to man-in-the-middle attacks, where the third party can intercept communications, appearing as a valid participant in the communication while changing or stealing information.
Rivest Shamir Adleman (RSA):
RSA, which is patented in 1983 and still the most widely-used system for digital security, was released the same year as Diffie-Hellman, and was named after its inventors, Ron Rivest, Adi Shamir, and Leonard Adleman. RSA gets much of its added security by combining two algorithms: one is applied to asymmetric cryptography, or PKI (Public Key Infrastructure), and the other algorithm provides for secure digital signatures. While the essential mathematics of both components is similar, and the output keys are of the same format.
The RSA algorithm has three main processes: key pair generation, encryption and decryption. Key pairs include the generation of the public key and the private key. Because of this part of the process, RSA has often been described as the first public-key digital security system. Once the public key is generated, it is transmitted over an unsecured channel, but the private key remains secret and is not shared with anyone. The data is encrypted with the public key, but can only be decrypted with the private key.
The keys are generated by multiplying large prime numbers. Since, as we noted, it is fast and easy to multiply even larger numbers, prime number encryption became a standard through several decades. To add a layer of security a method of obtaining digital signatures was an additional improvement in RSA. In this scenario – to simplify the process – the sender produces a hash value of the message, which uses the same exponentiation as the encryption number. The receiver applies does the same hash value at the receiving end to arrive at the same number, confirming the secured signature.
Other protocols rely on RSA digital signatures, so RSA has had a lot of staying power in the security world as other certification and security schemes have piggybacked onto it. However, RSA digital signature has a vulnerability, which will result in brute-force attacks being able to decode the private key; and exposed to specific attack types such as side-channel analysis, timing attacks, and others.
In addition, there is computational overhead involved in RSA, and particularly in mobile and tablet environment, as a result, the performance issue is a great deal. Key length is also a concern, as RSA keys now must be 2048-bit long, because given advances in cryptography and computing resources, 1024-bit keys were deemed insufficiently secure against several attacks. Government and many other organizations are now requiring a minimum key length of 2048-bits.
Digital Signature Algorithm (DSA):
In 1991, the National Security Agency (NSA) developed the Digital Signature Algorithm (DSA) as an alternative to the RSA algorithm. The National Institute of Standards and Technology (NIST) gave the algorithm its sanction as U.S. government-approved and -certified encryption scheme that offered the same degree of security as RSA, but employs different mathematical algorithms for signing and encryption.
Like RSA, DSA is an asymmetric encryption scheme, or PKI, which generates a pair of keys, one public and one private. The signature is created privately, though it can be identified publicly; the benefit of this is that only one authority can create the signature, but any other party can validate the signature using the public key. DSA, as a result, is faster in signing, but slower in verifying; hence, DSA is a sensible choice if there are more performance issues on the client side. DSA and RSA can be run together under some server systems like Apache, providing additional protection.
However, being so similar, DSA and RSA are subject to similar attacks, and RSA has moved to longer keys, which DSA has not yet done. While creating longer DSA keys is theoretically possible, it is not yet being done, so despite being very comparable in other ways to RSA, RSA remains the preferred encryption scheme.
ECC and ECDSA:
Harry potter minecraft map download. Elliptic Curve Cryptography (ECC) or Elliptic Curve Digital Signature Algorithm (ECDSA) was known and studied in the world of mathematics for 150 years before being applied to cryptography; Neal Koblitz and Victor S. Miller originally suggested it in 1985. However, in 2005, the NSA released a new set of U.S. government-endorsed security algorithms that also included ECC, in a release entitled “Suite B”.
Elliptic curve cryptography is a new cryptographic algorithm that has been developed for increased security and more robust network performance. Some researchers have claimed that ECC cryptography can provide as much strong security with a 164-bit key as other systems achieve with a 1024-bit key. With the advent of mobile devices being used for highly private transactions, more secure, low-overhead encryption schemes are becoming highly desirable. ECC cryptography helps to establish a level security equal to or greater than RSA or DSA, the two most widely-adopted encryption methods – and it does it with less computational overhead, requiring less processing power, and moving well beyond the mobile sphere in implementation.
ECDSA (Elliptic Curve Digital Signature Algorithm) is based on DSA, but uses yet another mathematical approach to key generation. ECC is a mathematical equation taken on its own, but ECDSA is the algorithm that is applied to ECC to make it appropriate for security encryption. Like RSA and DSA, it is another asymmetric cryptographic scheme, but in ECC, the equation defines the public/private key pair by operations on points of elliptic curves, instead of describing it as the product of very large prime numbers.